Max Weinreich



About me

I am a Lecturer at Harvard University. My research is in algebraic dynamics, a field at the intersection of dynamical systems, algebraic geometry, and number theory. I received my Ph. D. from Brown University in May 2022, advised by Joe Silverman. I held an NSF Mathematical Sciences Postdoctoral Research Fellowship from 2022-2025, supervised by Laura DeMarco.

My particular interests include dynamical degrees, billiards, moduli spaces, integrable systems, finite fields, symplectic maps, and projective configurations. Right now, I am working on projects related to irreducibility of plane curves and conformally symplectic maps on spaces of pentagons and hexagons.

I am on the tenure-track job market for jobs that start in Fall 2026.

Pronouns: he/him

Curriculum Vita (CV)

Contact Info

Email: mweinreich [at] math [dot] harvard [dot] edu

Papers

9. Degree growth of skew pentagram maps. Preprint, 34 pages plus code, 2025.

8. Configurations of 10 points and their incidence varieties. With Kelly Isham, Nathan Kaplan, Sam Kimport, Rachel Lawrence, and Luke Peilen. Preprint, 25 pages plus code, 2025.

7. Algebraic billiards in the Fermat hyperbola. Advances in Mathematics, 2025. 53 pages. (arxiv)

6. The dynamical degree of billiards in an algebraic curve. Journal of Geometric Analysis, 2024. 61 pages. (arxiv) (talk video)

5. GIT stability of linear maps on projective space with marked points. Illinois Math Journal, 46 pages, 2024. (arxiv)

4. Dynamical moduli spaces and polynomial endomorphisms of configurations. With Talia Blum, John Doyle, Trevor Hyde, Colby Kelln, and Henry Talbott. Arnold Math Journal, 33 pages, 2022. (arxiv)

3. The algebraic dynamics of the pentagram map. Ergodic Theory and Dynamical Systems, 46 pages, 2022. (arxiv)

2. Automorphism groups of endomorphisms of P^1(F_p). With Julia Cai and Benjamin Hutz and Leo Mayer. Glasgow Math Journal, 34 pages, 2022. (arxiv)

1. Counting arcs in projective planes via Glynn's algorithm. With Nathan Kaplan, S. Kimport, Rachel Lawrence, and Luke Peilen. Journal of Geometry, 17 pages, 2017. (arxiv)


About my math

The image shows a three-circle Venn diagram. The intersection of Algebraic Geometry and Dynamical Systems is Algebraic Dynamics. The intersection of Algebraic Geometry and Number Theory is Arithmetic Geometry. The intersection of Number Theory and Dynamical Systems is Arithmetic Dynamics. My research is in the triple intersection.

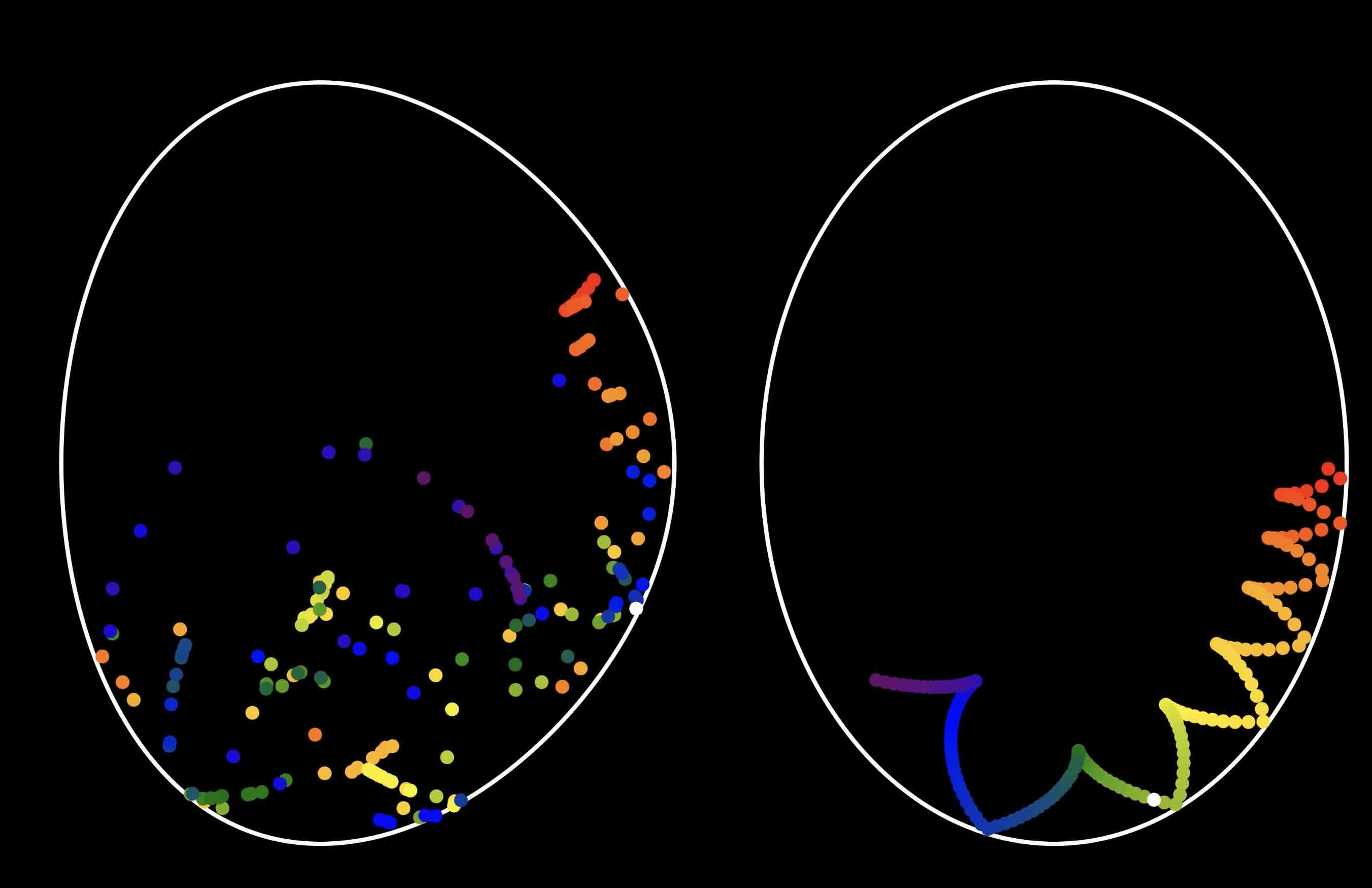
My recent work is on billiards in algebraic curves. Watch a video that illustrates my work!

The onset of chaos in the billiard inside an elliptic curve, but not an ellipse.

Notes

Topics course notes on dynamical degrees

Mapping classes and character varieties

Julia sets in Berkovich space

NSF Information

My work from 2022-2025 was supported by NSF Grant No. 2202752. My graduate work was supported by NSF Grant No. 2040433.